履帶式起重性能是各類工程起重設(shè)備吊裝作業(yè)的關(guān)鍵性指導(dǎo)依據(jù)之一，其設(shè)置的準(zhǔn)確及合理性將直接影響起重設(shè)備的安全可靠性。就履帶起重機(jī)而言，起重性能計(jì)算需要重點(diǎn)關(guān)注臂架強(qiáng)度、整機(jī)穩(wěn)定性及各受力部件性能( 拉板承載能力、變幅能力、單繩拉力、起升倍率) 等因素的綜合影響，核算每個(gè)限制條件下起重機(jī)能夠承受的大載荷，從大承受載荷中獲取小值作為額定起重性能，形成起重量表。關(guān)于履帶式起重機(jī)設(shè)計(jì)，不同國(guó)家或區(qū)域出臺(tái)了相關(guān)設(shè)計(jì)準(zhǔn)則或規(guī)

范，如我國(guó)的GB 3811—2008《起重機(jī)設(shè)計(jì)規(guī)范》、歐洲的EN 13000—2014《起重機(jī)移動(dòng)式起重機(jī)》等。探究和解析目前市場(chǎng)成熟產(chǎn)品起重性能存在的分布規(guī)律，可為產(chǎn)品研發(fā)、改進(jìn)及工程應(yīng)用中起重量的預(yù)判、規(guī)劃和掌控提供重要參考。本文對(duì)歐美兩個(gè)品牌履帶式起重機(jī)系列產(chǎn)品起重量進(jìn)行分析。首先，通過(guò)MATLAB獲得歐洲產(chǎn)品起重量數(shù)據(jù)的變化趨勢(shì)，進(jìn)行數(shù)據(jù)擬合確定函數(shù)關(guān)系，再通過(guò)北美產(chǎn)品進(jìn)行驗(yàn)證，從而獲得可靠性較高的分析結(jié)果。

1 起重量分析及評(píng)價(jià)

1． 1 起重量分析

     選用歐洲某履帶起重機(jī)系列產(chǎn)品起重量作為基礎(chǔ)進(jìn)行分析，包括100 t、200 t( 中小噸位) 、300 t、400 t( 中噸位) 、500 t、600 t( 中大噸位) 等系列產(chǎn)品，覆蓋了工程領(lǐng)域常用的產(chǎn)品系列。下面以100 t 產(chǎn)品主臂工況起重量說(shuō)明分析過(guò)程。歐洲某品牌100 t 履帶起重機(jī)主臂起重量見(jiàn)表1。

表1 歐洲某品牌100 t 履帶起重機(jī)主臂起重量表( 部分) t作業(yè)幅( m)臂長(zhǎng)( m)

    起重量數(shù)據(jù)分析過(guò)程中，以臂長(zhǎng)分組將相應(yīng)作業(yè)幅度起重量應(yīng)用多項(xiàng)式、冪函數(shù)、倒冪函數(shù)、指數(shù)函數(shù)、雙曲線函數(shù)等擬合考察其變化趨勢(shì)，發(fā)現(xiàn)多項(xiàng)式( 式1) 、指數(shù)函數(shù)( 式2) 、倒冪函數(shù)( 式3) 等能夠?qū)ζ鹬亓繑?shù)據(jù)進(jìn)行較好描述:f( x) = pn?xn + pn － 1?xn － 1… + p1?x + p0 ． ( 1)其中: n 為函數(shù)高次數(shù)，n = 1，2

，3…; pn為n 次項(xiàng)對(duì)應(yīng)系數(shù)。f( x) = a?ebx + c?edx ． ( 2)其中: a、b、c、d 為系數(shù)。f( x) = p1 /( x2 + q1?x + q2) ． ( 3)

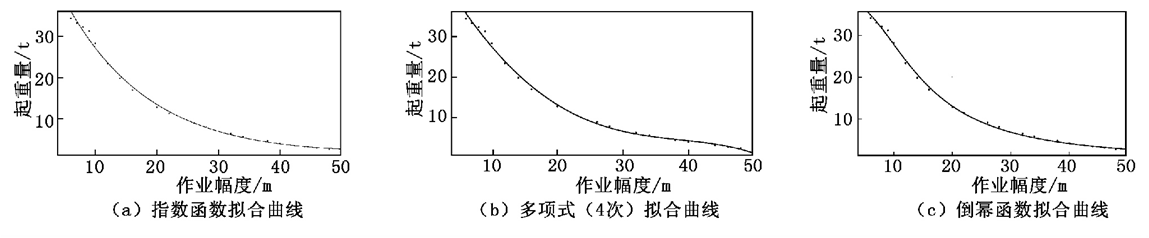
其中: p1、q1、q2為系數(shù)。在MATLAB 軟件中應(yīng)用上述三種函數(shù)進(jìn)行數(shù)據(jù)擬合分析，主要方式有兩種: 一種是用函數(shù)命令擬合，該法較繁瑣; 另一種是用曲線擬合工具包Curve FittingTool 在圖形窗口操作，具有簡(jiǎn)便、快速、可操作性強(qiáng)的優(yōu)點(diǎn)［2］。本文采用工具包Curve Fitting Tool 進(jìn)行數(shù)據(jù)處理，將100 t 產(chǎn)品起重量按不同臂長(zhǎng)導(dǎo)入MATLAB軟件，采用上述函數(shù)逐一進(jìn)行擬合，可獲得每個(gè)臂長(zhǎng)下起重量隨著工作幅度變化的擬合曲線。100 t 履帶起重機(jī)主臂50 m 的擬合曲線如圖1 所示。

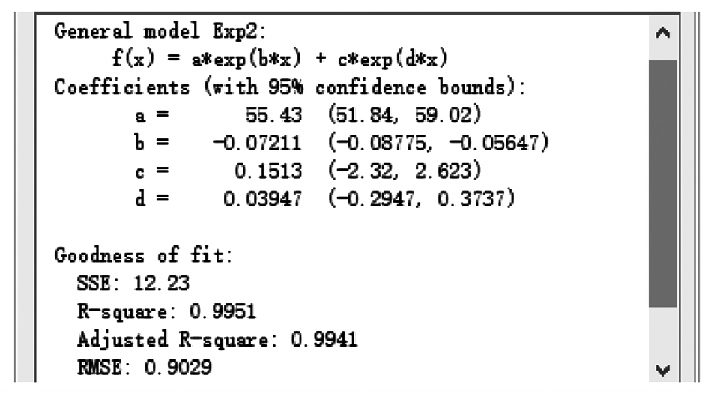
圖1 100 t 履帶起重機(jī)主臂50 m 的擬合曲線圖1 顯示，對(duì)于100 t 履帶起重機(jī)主臂50 m 工況，指數(shù)函數(shù)、多項(xiàng)式函數(shù)( 4 次) 、倒冪函數(shù)均能夠較好地逼近起重量隨著幅度增大呈現(xiàn)的變化趨勢(shì)，除10 m 內(nèi)小幅度起重量與擬合曲線存在偏差，其他起重量均與擬合曲線相近或重合。為表征函數(shù)擬合效果，MATLAB 工具包Curve Fitting Tool 提供了評(píng)價(jià)參數(shù)，如圖2 所示。

圖2 中，上部為指數(shù)函數(shù)擬合所得系數(shù)值，下部為擬合效果評(píng)價(jià)參數(shù)值。圖2 曲線擬合工具箱擬合效果評(píng)價(jià)指標(biāo)( 100 t 產(chǎn)品主臂50 m)MATLAB 工具包Curve Fitting Tool 提供的評(píng)價(jià)參數(shù)主要包含SSE、Ｒ-square、ＲMSE 等。( 1) SSE( 和方差) : 表征起重量擬合數(shù)據(jù)和原始數(shù)據(jù)對(duì)應(yīng)點(diǎn)的誤差平方和。其表達(dá)式為:SSE =Σmi = 1( yi－ y'i) 2 ． ( 4)其中: yi為原始起重量數(shù)據(jù); y'i為擬合起重量數(shù)據(jù); m為數(shù)據(jù)總數(shù)量，i = 1，2，3，…，m。SSE 越趨于0，表明

擬合程度與函數(shù)選擇越佳。

( 2) Ｒ-square ( 確定系數(shù)) : Ｒ-square 由誤差平方和( 預(yù)測(cè)數(shù)據(jù)與原始數(shù)據(jù)均值之差的平方和) 與標(biāo)準(zhǔn)差( 原始數(shù)據(jù)和均值之差的平方和) 比值決定。其表達(dá)式為:

Ｒ-square = 1 －Σmi =1( yi － y'i) 2 /Σmi =1( yi － ( yi

－ ) ) ． 

( 5)其中: yi－ 為原始起重量均值。Ｒ-square 值正常取值范圍為0 ～ 1，比值越趨近1，表明估計(jì)值與實(shí)際值越接近，數(shù)據(jù)擬合效果越好。

( 3) ＲMSE( 均方根誤差) : 均方根誤差對(duì)測(cè)量數(shù)據(jù)中特大或特小誤差反應(yīng)敏感，能夠很好地反映出測(cè)量的精密度。其表達(dá)式為:ＲMSE = 1mΣni = 1( yi － y'i) 槡2 ．

 ( 6)表2 和表3 分別為100 t 和400 t 履帶起重機(jī)起重量( 部分) 采用4 次多項(xiàng)式擬合得到的擬合評(píng)價(jià)參數(shù)。由于履帶起重機(jī)噸位跨度大，采用數(shù)值如SSE 值表征擬合效果時(shí)不同噸級(jí)履帶起重機(jī)存在較大差異，如100 t 產(chǎn)品26 m 主臂與400 t 產(chǎn)品28 m 主臂起重量，SSE 值分別為5． 334 和31． 79，但實(shí)際上前者Ｒ-square值為0． 999 3 比后者的0． 999 7 還略差。因此，起重量基數(shù)的差異可能會(huì)使數(shù)值型評(píng)價(jià)參數(shù)數(shù)值放大，影響評(píng)價(jià)直觀性，故本文后續(xù)采用Ｒ-square 值進(jìn)行評(píng)價(jià)。表2 100 t 產(chǎn)品起重量( 部分) 擬合評(píng)價(jià)參數(shù)( 4 次多項(xiàng)式)臂長(zhǎng)( m) SSE Ｒ-square ＲMSE

表3 400 t 產(chǎn)品起重量( 部分) 擬合評(píng)價(jià)參數(shù)( 4 次多項(xiàng)式)臂長(zhǎng)( m) SSE Ｒ-square ＲMSE21

1． 2 起重量擬合評(píng)價(jià)

按照上述方法，對(duì)歐洲某品牌100 t ～ 600 t 系列履帶起重機(jī)全部起重量進(jìn)行數(shù)據(jù)擬合，獲得每個(gè)產(chǎn)品各臂長(zhǎng)Ｒ-square 值，并求取均值及標(biāo)準(zhǔn)差，得到的數(shù)據(jù)見(jiàn)表4。

其中深色數(shù)據(jù)為同組中佳數(shù)據(jù)。表4 歐洲品牌主臂起重量擬合評(píng)價(jià)參數(shù)噸級(jí)擬合函數(shù)Ｒ-square 值多項(xiàng)式指數(shù)函數(shù)倒冪函數(shù)指標(biāo)中小噸位中噸位中大噸位

表4 數(shù)據(jù)顯示: ①三種函數(shù)均能描述起重量變化趨勢(shì)，結(jié)合Ｒ-square 值可知4 次多項(xiàng)式和指數(shù)函數(shù)擬合效果更佳;

 ②從噸位級(jí)別來(lái)看，中小噸位產(chǎn)品4 次多項(xiàng)式擬合數(shù)據(jù)效果較好，中噸位產(chǎn)品盡管300 t 產(chǎn)品指數(shù)函數(shù)的Ｒ-square 值佳，但數(shù)據(jù)離散程度略大，多項(xiàng)式與倒冪函數(shù)Ｒ-square 值的均值及標(biāo)準(zhǔn)差相當(dāng)，綜合整體情況可采用4 次多項(xiàng)式進(jìn)行數(shù)據(jù)擬合，中大噸位產(chǎn)品指數(shù)函數(shù)擬合較好。為驗(yàn)證上述結(jié)論，選用北美某產(chǎn)品對(duì)4 次多項(xiàng)式及指數(shù)函數(shù)擬合效果進(jìn)行驗(yàn)證，擬合評(píng)價(jià)參數(shù)見(jiàn)表5。其中深色數(shù)據(jù)為同組中佳數(shù)據(jù)，該產(chǎn)品系列中無(wú)500 t 產(chǎn)品。

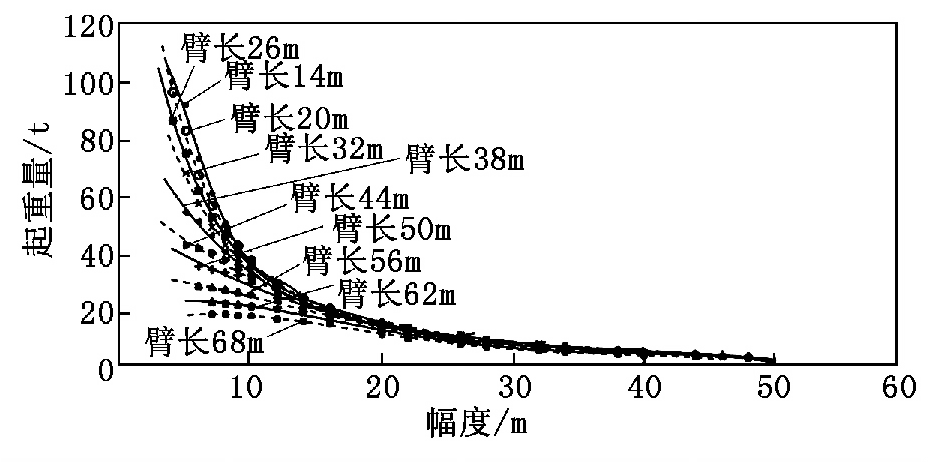
表5 北美某品牌起重機(jī)主臂起重量擬合評(píng)價(jià)參數(shù)噸級(jí)擬合函數(shù)Ｒ-square 均值4 次多項(xiàng)式指數(shù)函數(shù)中小噸位表5 數(shù)據(jù)顯示，前文結(jié)論得到有效驗(yàn)證。綜上，中噸位及中小噸位產(chǎn)品可采用4 次多項(xiàng)式描述，中大噸位產(chǎn)品可采用指數(shù)函數(shù)描述。將表1 中歐洲100 t 產(chǎn)品全部起重量數(shù)據(jù)繪制散點(diǎn)圖并同時(shí)繪制每個(gè)臂長(zhǎng)下起重量4 次多項(xiàng)式擬合曲線，如圖3 所示。由圖3 可見(jiàn)，起重量按臂長(zhǎng)隨作業(yè)幅度增加依照4 次多項(xiàng)式曲線呈現(xiàn)非線性減小規(guī)律。

圖3 100 t 起重機(jī)起重量散點(diǎn)圖及變化規(guī)律2 

總結(jié)

本文通過(guò)對(duì)歐美兩品牌系列履帶起重機(jī)起重量進(jìn)行探析發(fā)現(xiàn)，隨著作業(yè)幅度的增加中噸位及中小噸位產(chǎn)品起重量依照4 次多項(xiàng)式、中大噸位產(chǎn)品起重量依照指數(shù)函數(shù)曲線呈逐漸減小規(guī)律。因此，在履帶式起重機(jī)設(shè)計(jì)及工程應(yīng)用中可以通過(guò)4 次多項(xiàng)式及指數(shù)函數(shù)對(duì)起重量進(jìn)行控制和判斷，具有良好的實(shí)踐指導(dǎo)價(jià)值，也為其他工程起重設(shè)備起重量的分析提供了思路。

期